In keeping with the linguistic theme, loan interest amounts to bunch of Non-Cents. True, some interest payments are tax-deductible, but you never get all of it back. Plus, if you didn’t owe money you would be able to better afford to pay taxes (and other expenses), and tax revenue is a necessary evil. But I digress. The main point here is that while interest payments have likely been around as long as money has been loaned to borrowers, therefore largely making interest a necessary practice, the manner in which interest is actually calculated borders on evil.
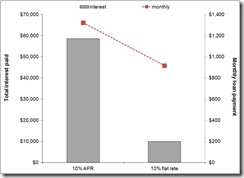For example, let’s consider a 10-year loan for $100,000 with a 10% annualized percentage rate (APR) vs. a loan where 10% of every minimum monthly payment went to pay loan interest. With the 10% APR loan, a monthly payment of $1,322 is used to pay off the loan in 10 years, but comes at a cost of $58,581 in interest payments. In comparison, if 10% of a fixed monthly principal payment was added as an interest payment, the loaner would still earn $10,000 in interest (in addition being able to re-loan the principal), but the borrower would save $48,581. The loaner doesn’t get as rich, but the borrower is considerably less poor, particularly since after the loan is paid off they have an ‘extra’ $916 each month for saving or covering other expenses.
The reason that so much more interest is paid with the APR approach is that the monthly interest payment is calculated as 1/12th of the annual interest payment that would be owed based on the loan balance for that month. So, for a $100,000 loan the annual interest payment at 10% would be $10,000, which divided by 12 would be $833. Thus, $833 (63%) of the first monthly payment of $1,322 would be for interest and the remainder is used to lower the loan balance. Slight but systematic reductions in the proportion of interest and increases in the proportion of principal are then associated with each monthly payment thereafter.
The next section provides more details and important considerations with respect to understanding APR and the total amount of interest paid.